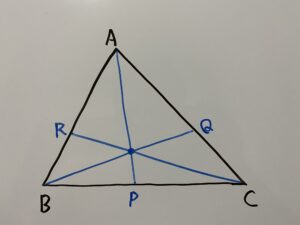
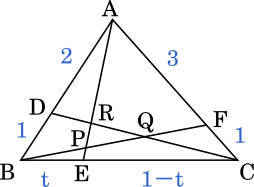
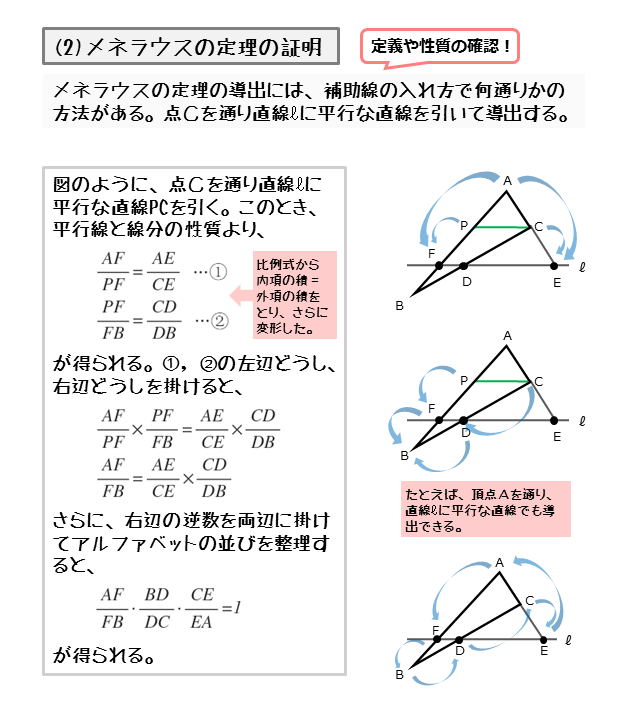
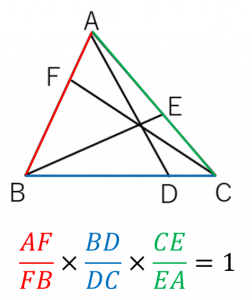
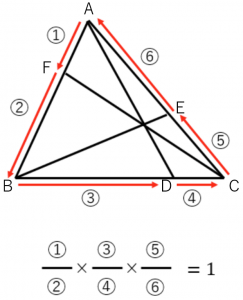
チェバの定理を使う問題(例題) 問題はこうじゃ 数学おじさん 上の図で、 AF BF = 3 2 AE CE = 1 2 のとき、 BD CD はなんでしょうか? トンちゃん なるほどだブー これはチェバの定理が使える図になってますね! そのとおりじゃ 上で説明した、チェバの定理が使える条件に当てはまっておるのぉ チェバの定理を覚え方の手順で、作り出すと、 A F B F × B D C D × C E A E = 1 と
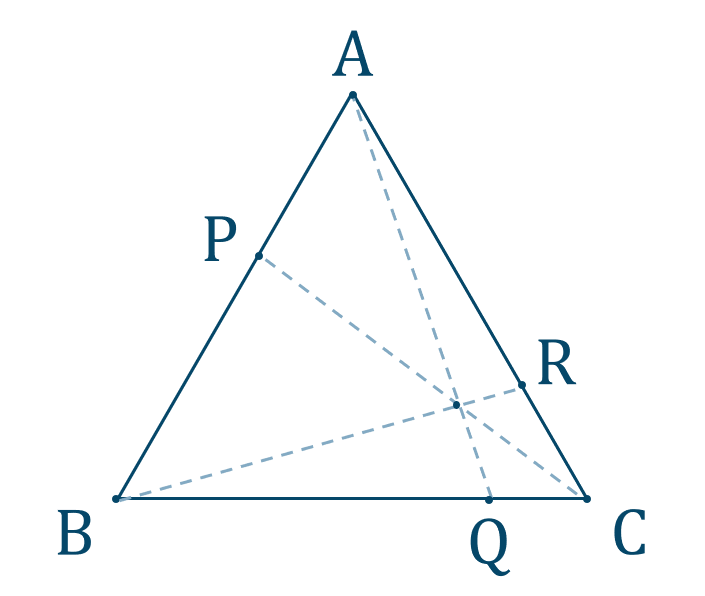
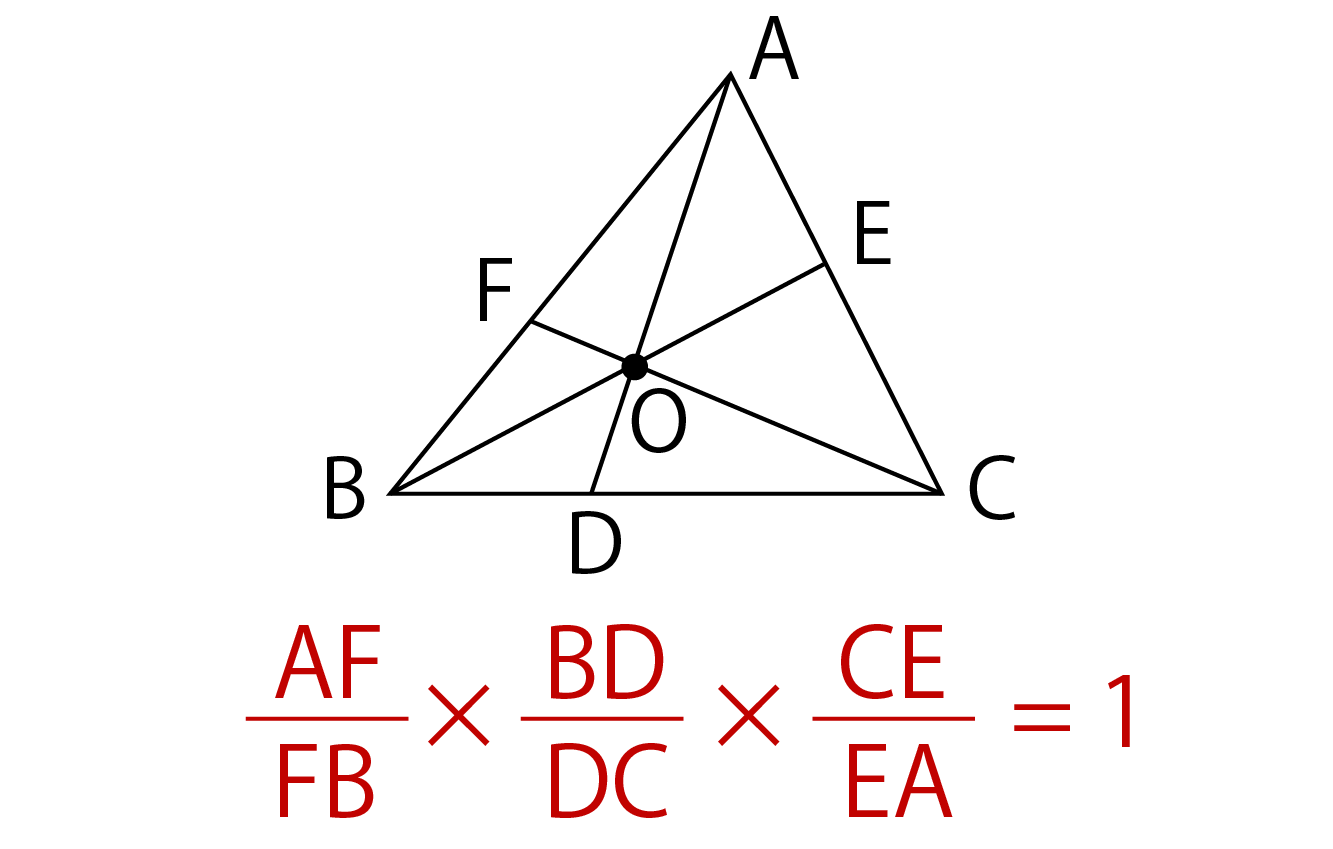
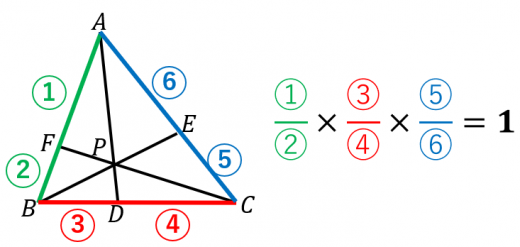
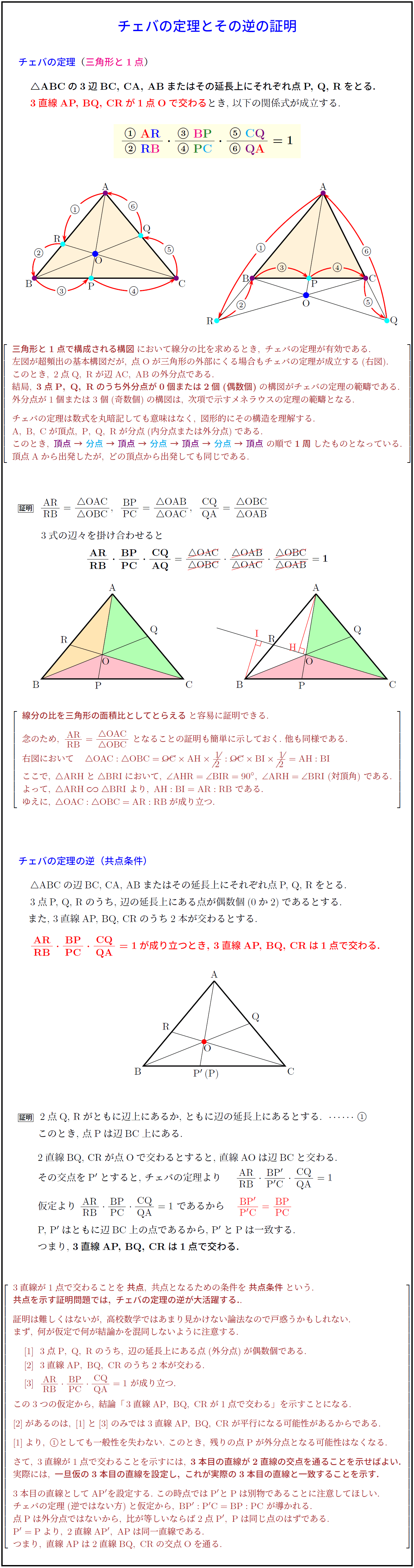
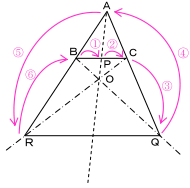
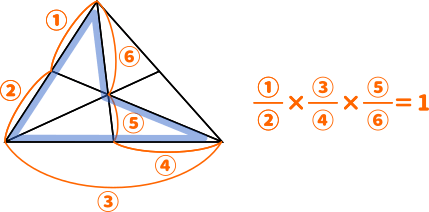
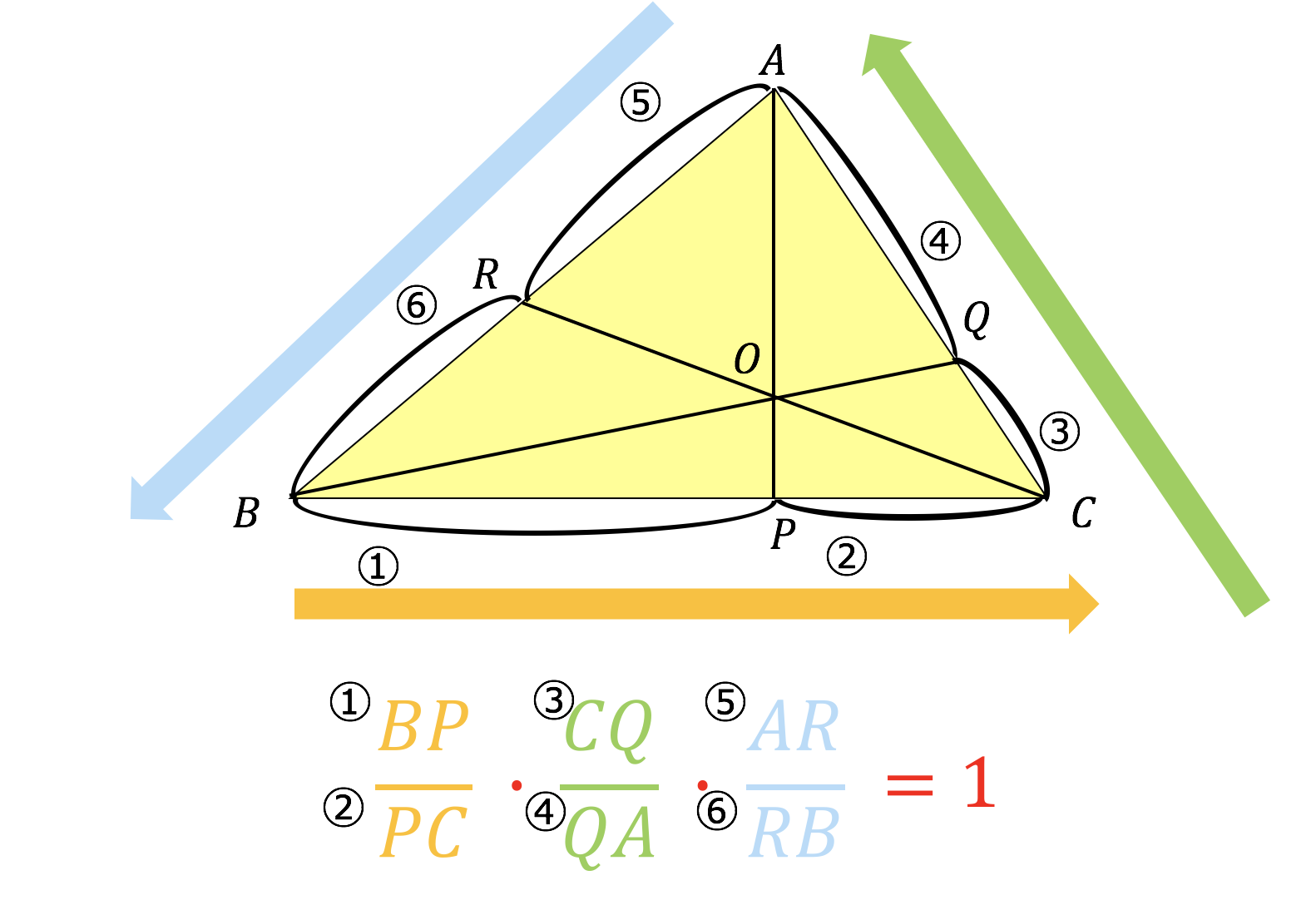
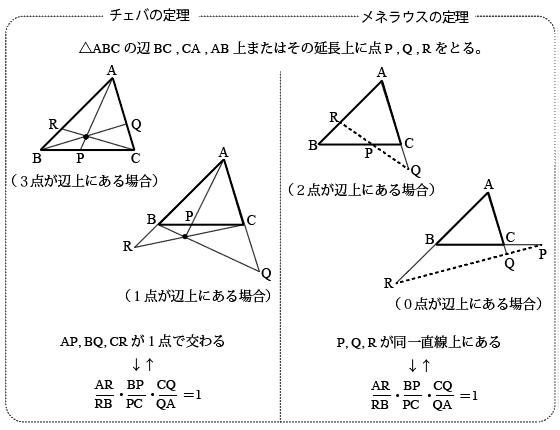
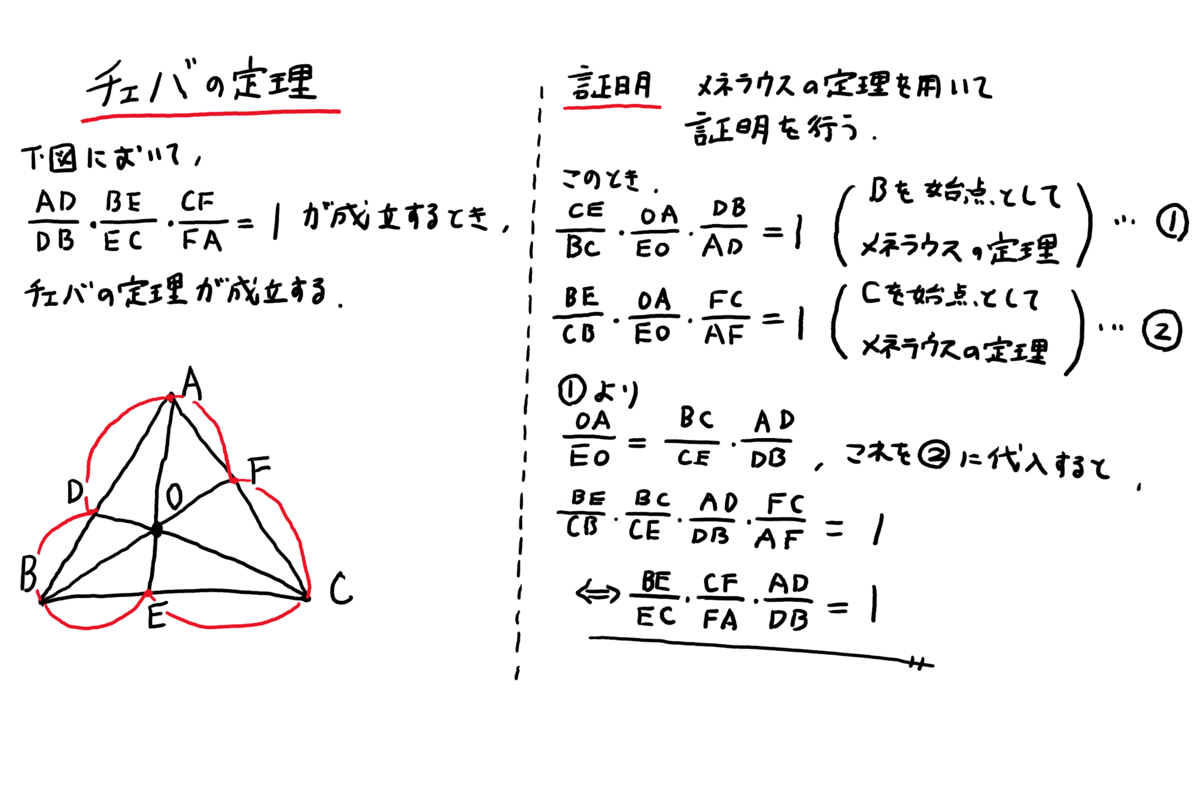
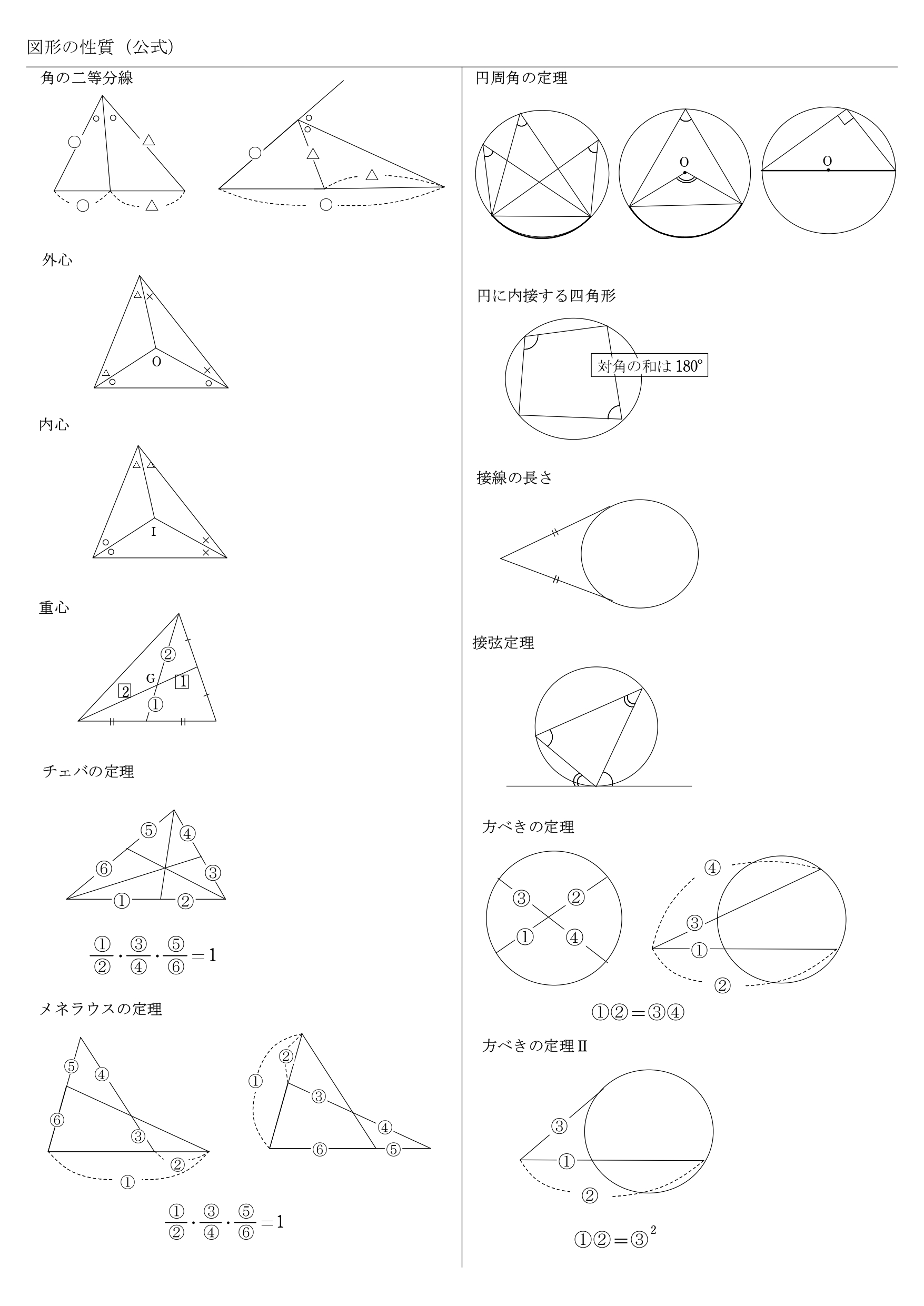
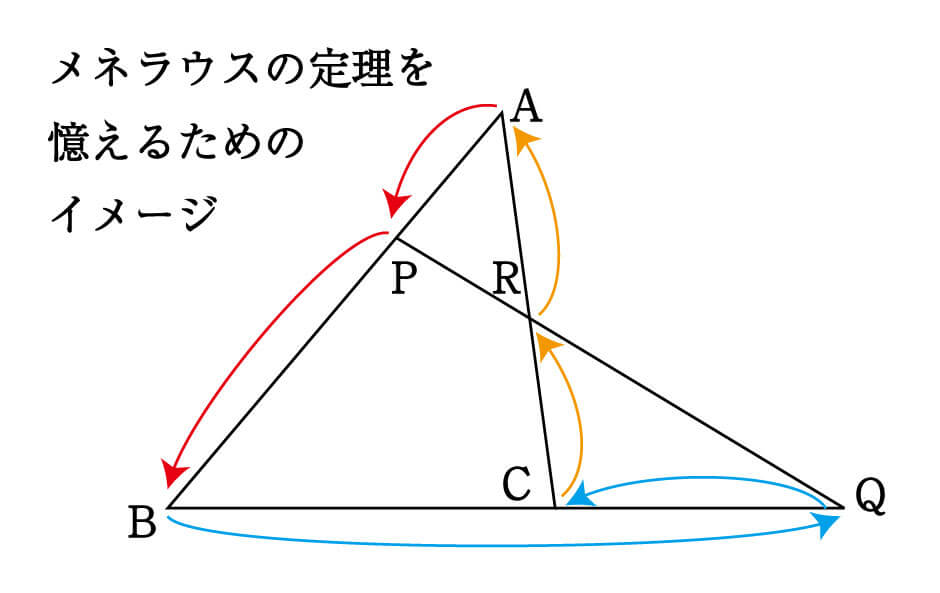
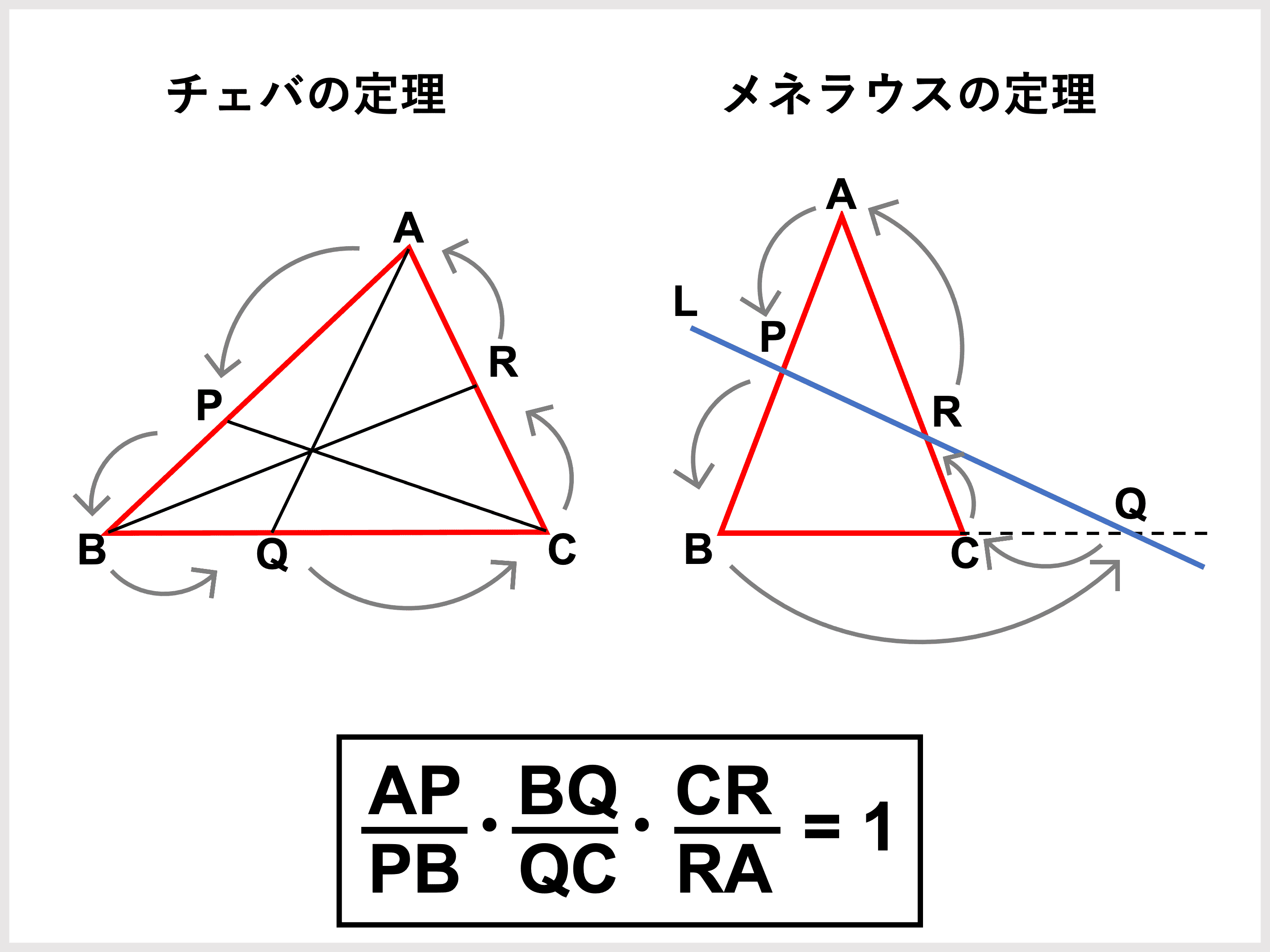
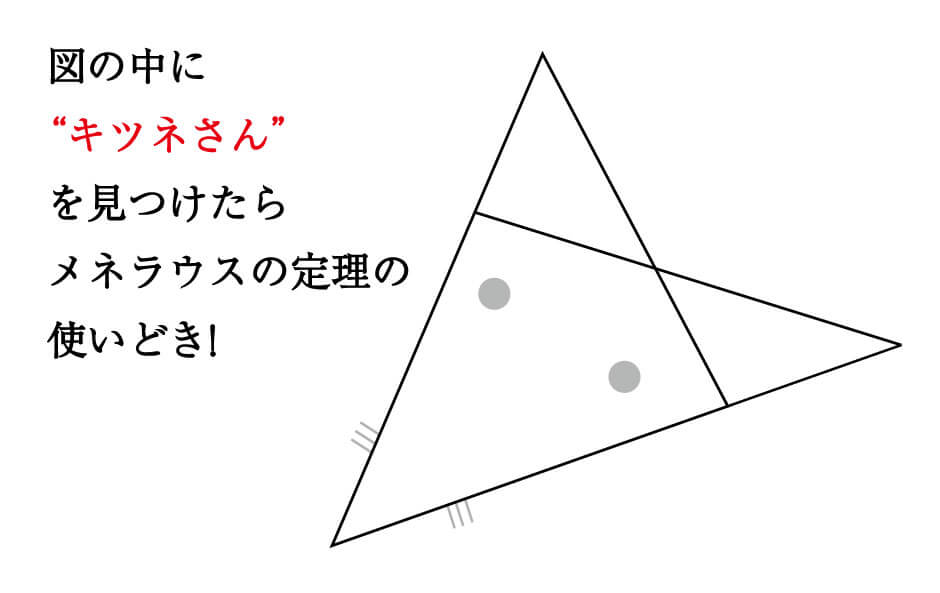
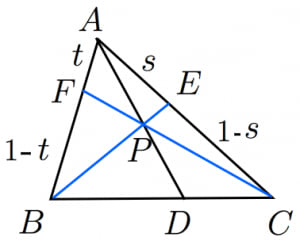
チェバの定理 証明 問題- チェバの定理の逆 abcの辺bc, ca, abまたはその延長上にそれぞれ点p,q,rがあり、この3点のうち辺の延長上にあるのは0または2個だとする。 このとき bqとcrが交わり、かつ bp pc ・ cq qa ・ ar rb =1 が成り立つなら3直線ap, bq, crは1点で交わる。 a b c p q r メネラウスの定理 なぜ「チェバ・メネラウスの定理の逆」は使用頻度が低いか? 基本的にベクトルを使えばこれらの定理を使うことはほとんどありません。 そしてベクトルを使わない平面図形の問題といえば 共通テスト数IAぐらいしかありません。 共通テストは数値を埋める形式であり,証明問題が出ていませんので「同一直線上にある」「1点で交わる」という結論の定理
チェバの定理 証明 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  | |
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | 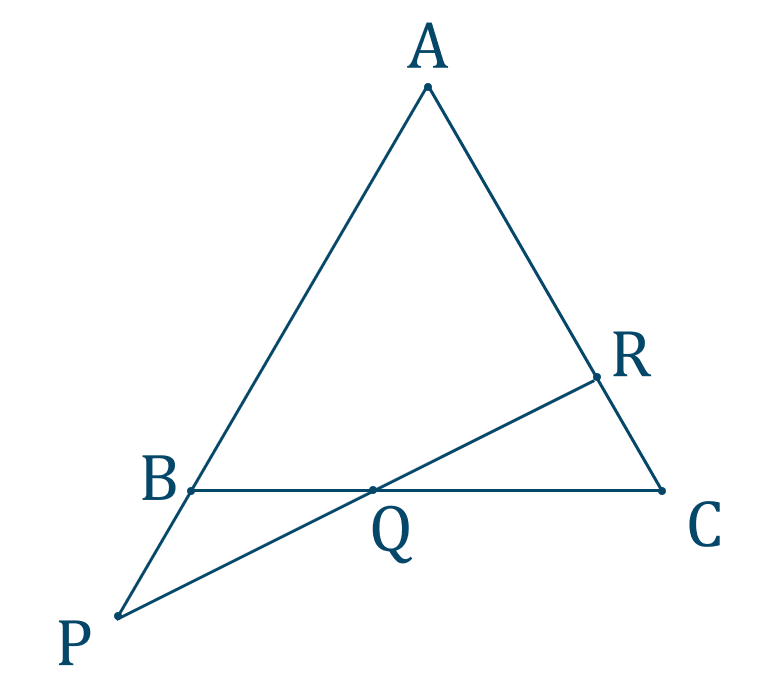 | |
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
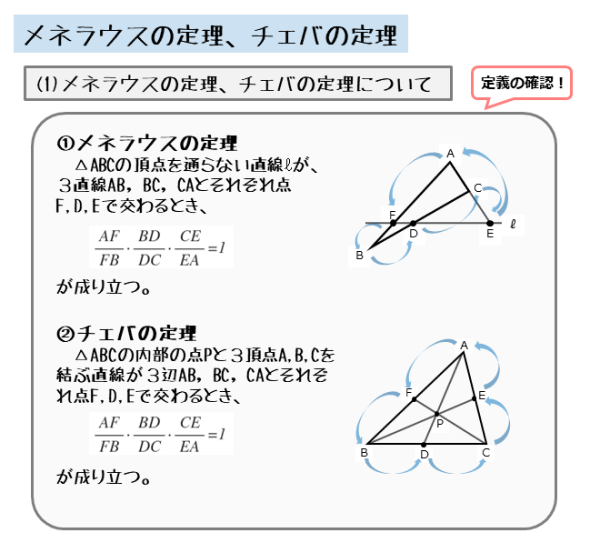 | 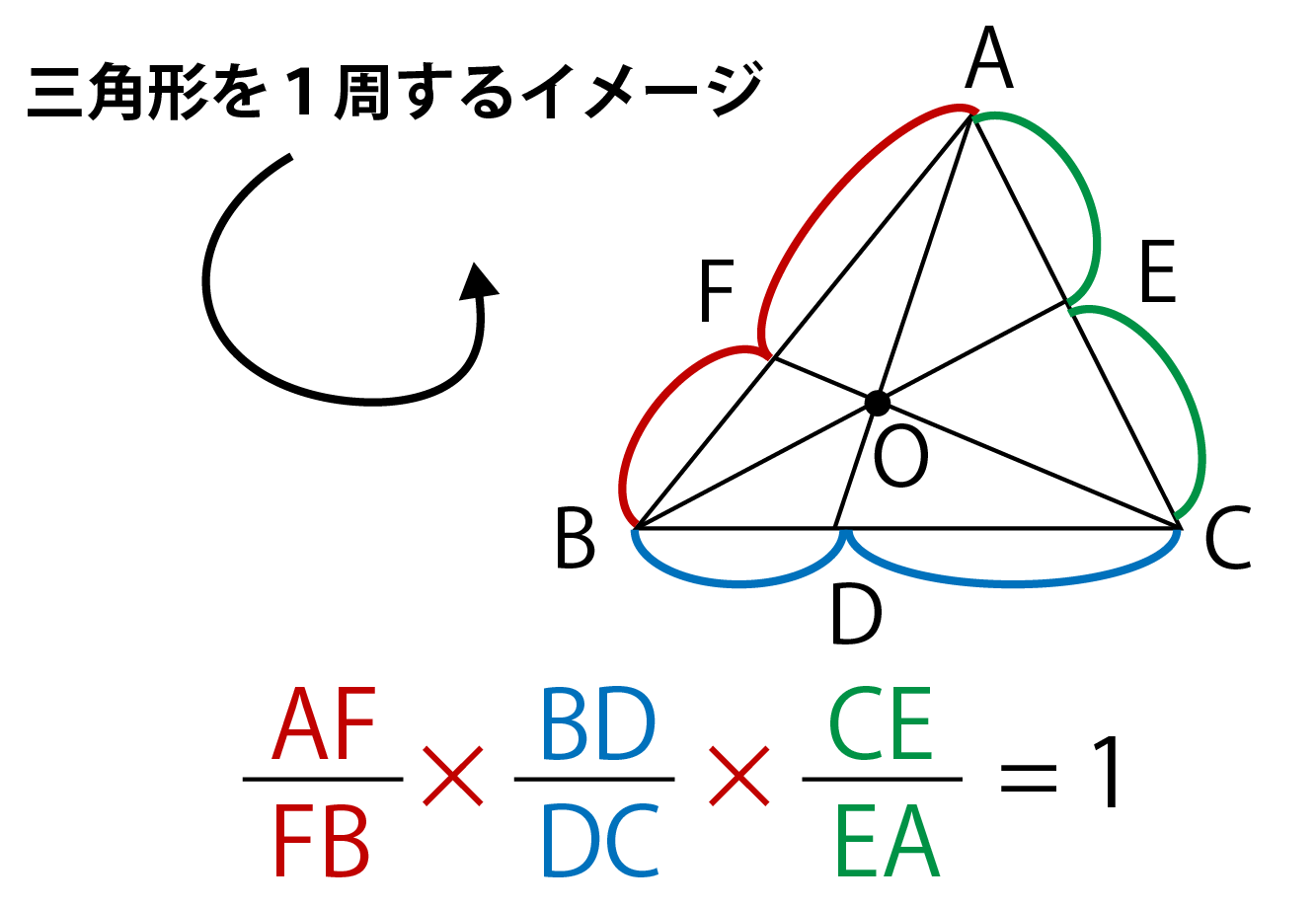 | 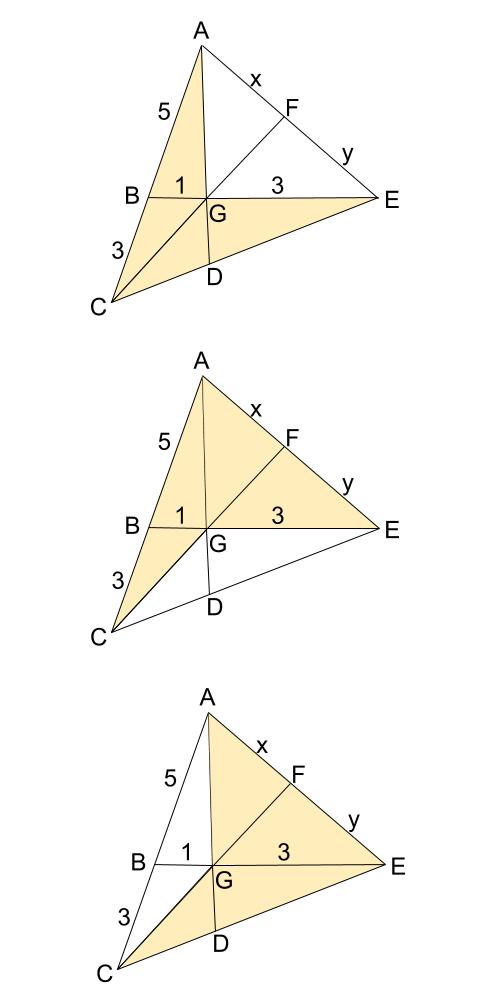 |
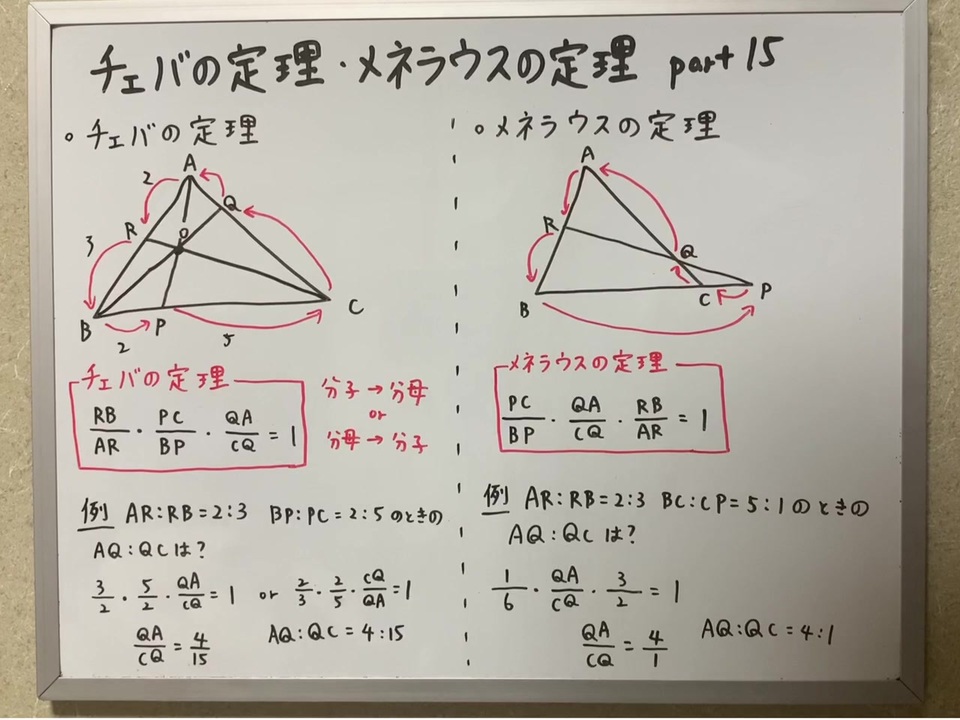 |  | |
「チェバの定理 証明 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
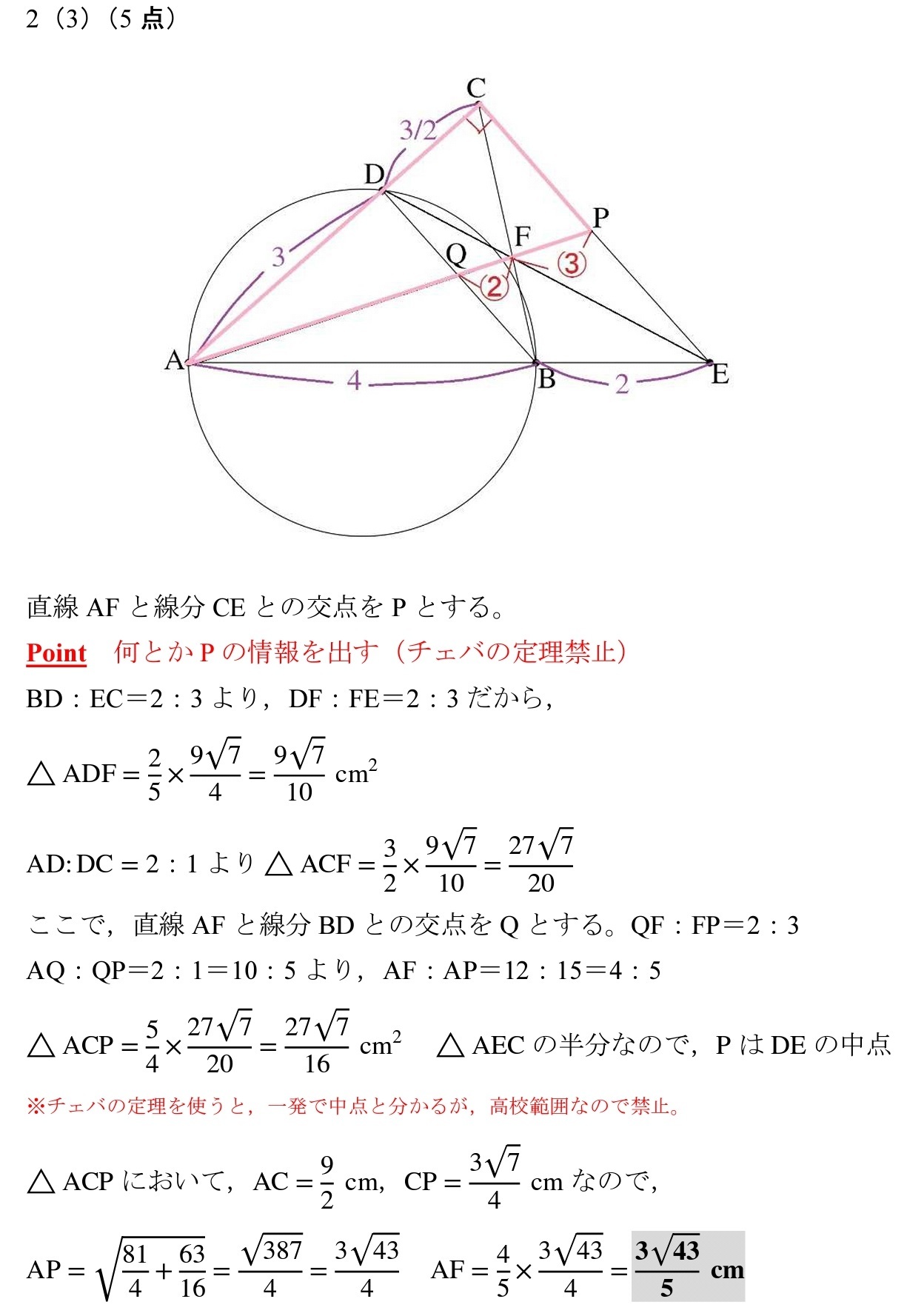
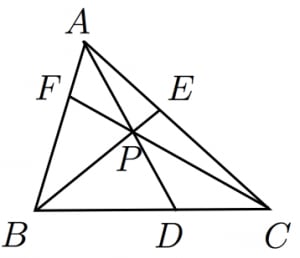
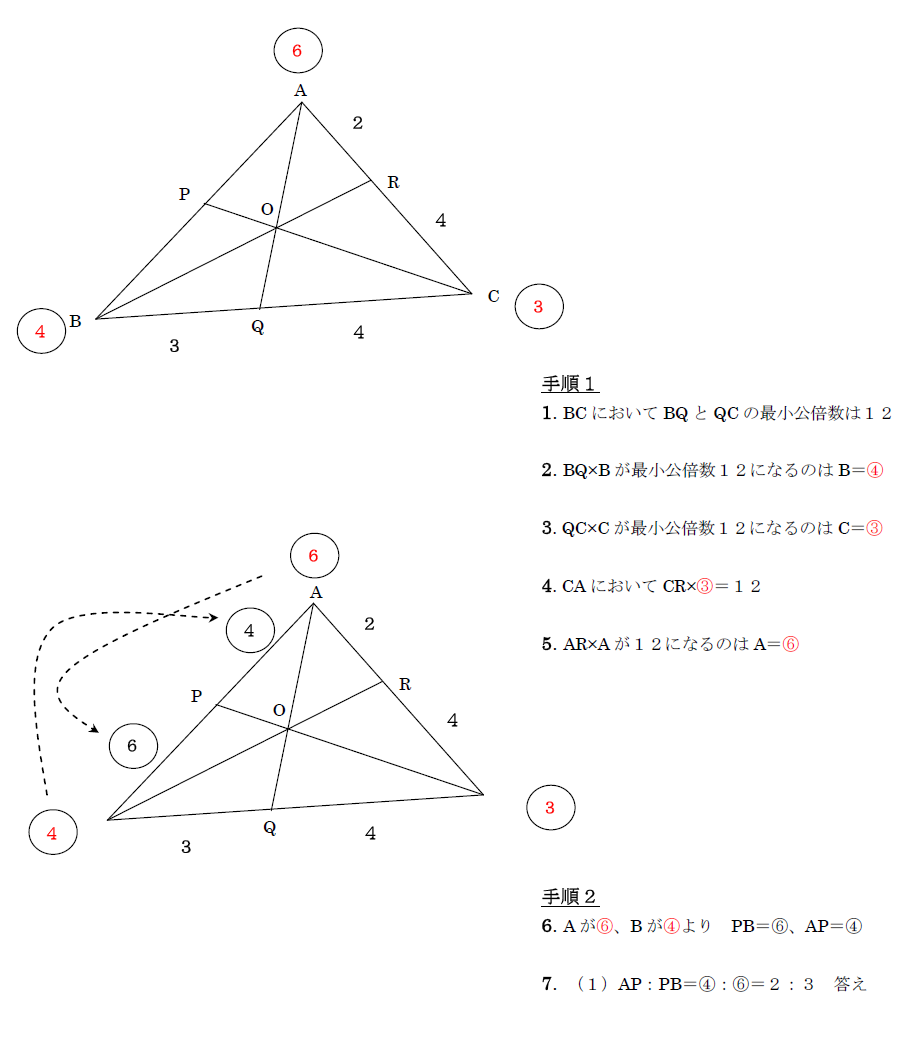
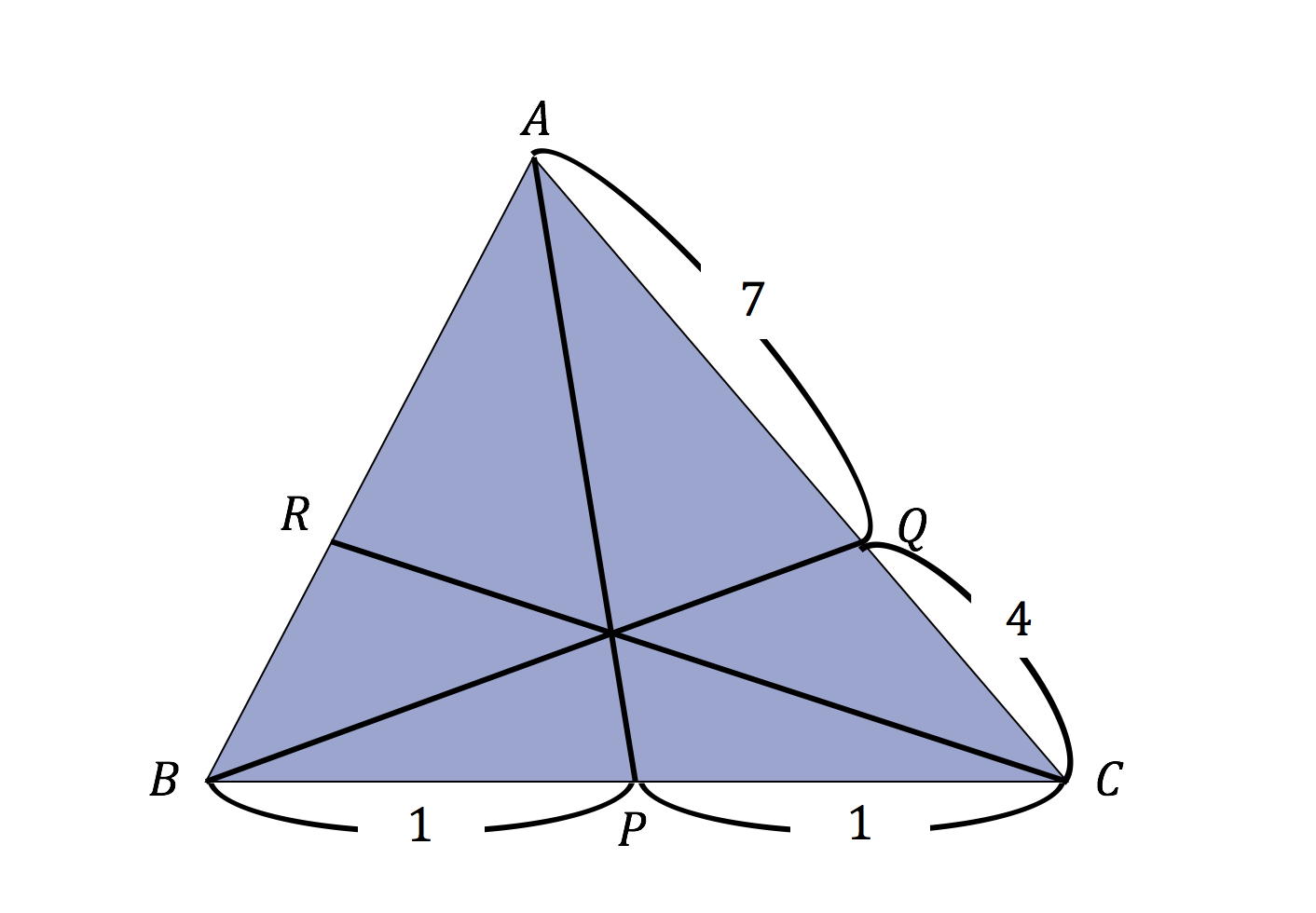
チェバの定理2応用に関する問題 この動画の問題と解説 練習 一緒に解いてみよう 解説 これでわかる! 練習の解説授業 三角形の面積比に関する問題だね。 この問題は、まずBP:PCの線分比を チェバの定理 で求めるのがポイントだよ。 POINT 「面積比」は「底辺と高さ」に注目 三角形の面積比 は、 底辺 と 高さ に注目するのが重要だったね。 ここで、「あっ」と気付くことができるかな? ABO では、問題を解きながら、チェバの定理を実際にどのように使うのか、一緒に見ていきましょう。 問題を解いてみよう! それでは、実際に問題を解いてみましょう。 例題 1辺の長さが7の正三角形ABCがあり、正三角形ABCの内部に点Oがあるとする。 直線AO、BO、COが対辺BC、CA、ABと交わる点をP、Q、RとするとAQ=6、AR=3であった。 このとき線分BPの長さを求めよ。 こ
Incoming Term: チェバの定理 問題, チェバの定理 問題集, チェバの定理 問題 応用, チェバの定理 難しい 問題, チェバの定理 メネラウスの定理 問題集, チェバの定理 証明 問題, メネラウスの定理 チェバの定理 問題, メネラウス チェバの定理 問題, 数学 チェバの定理 問題,




No comments:
Post a Comment