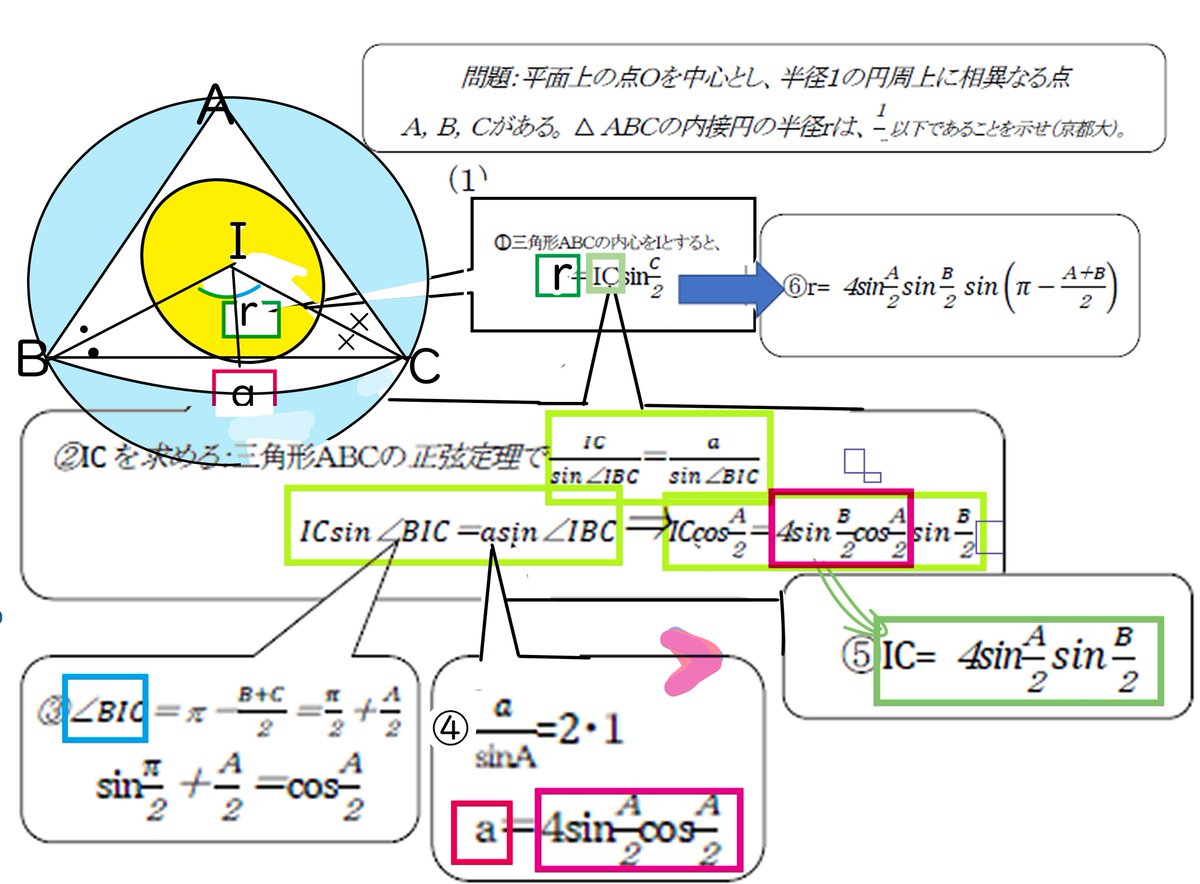
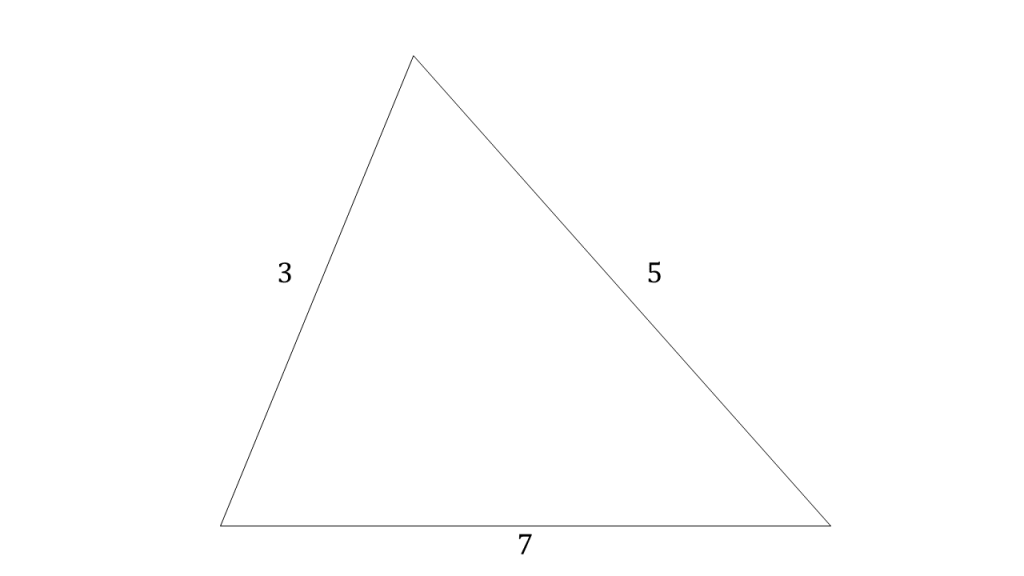
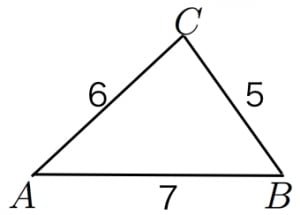
(再追記) 例6.において、ヘロンの公式の初等的証明を示したが、次のような証明がある ことを最近知った。 ヘロンの公式における s-a、s-b、s-c の意味が分かって、思わず唸って しまった。(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。この公式だと「3辺と内接円の半径から面積を計算する」ということをしています。 しかし、ヘロンの公式なら3辺から面積がわかります。 よって、3辺から内接円の半径を計算できることに気が付きます。さっそく計算してみると となります。
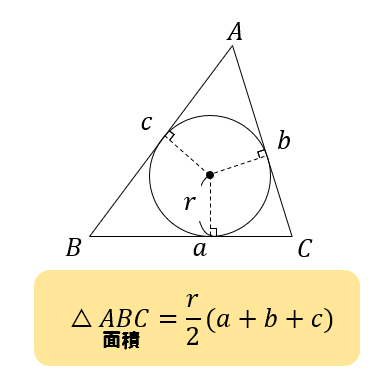
内接円の半径
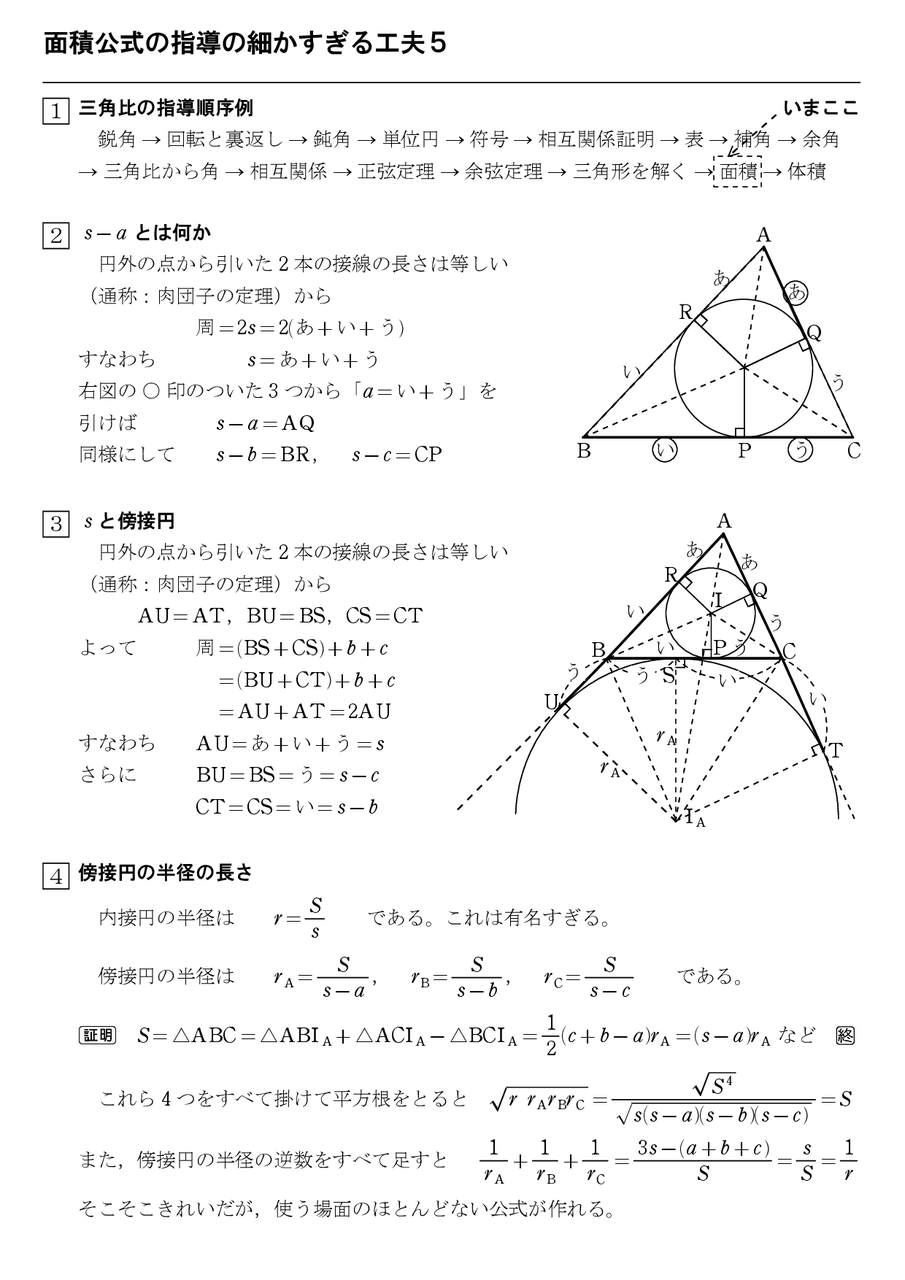
ヘロンの公式 証明 内接円
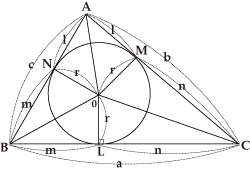
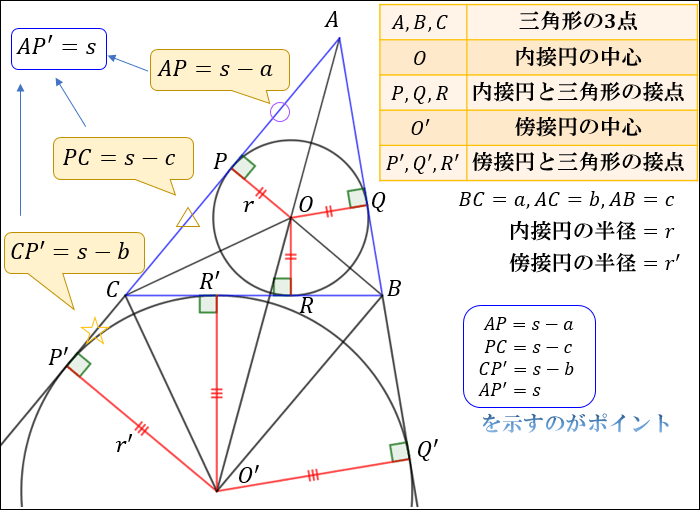
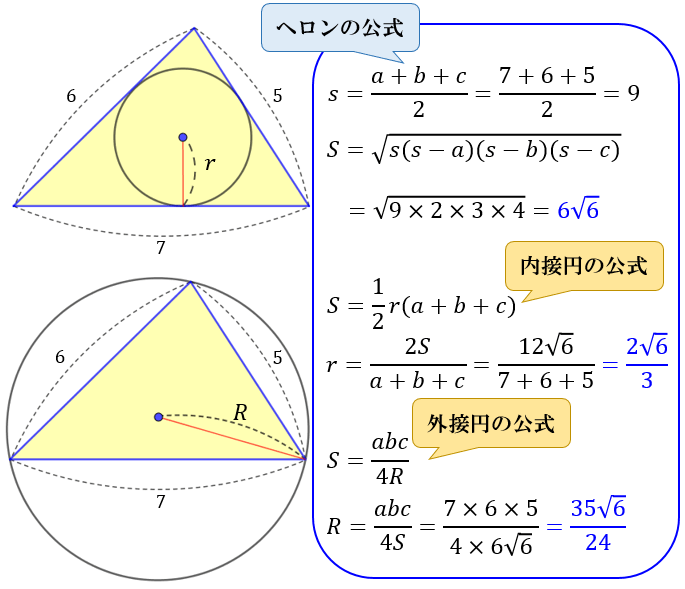
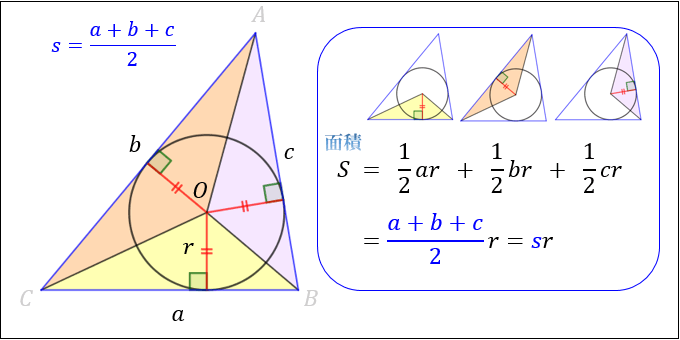
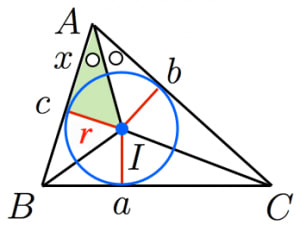
ヘロンの公式 証明 内接円-ABCの辺BCの外側に描いた傍接円において、頂点Aから引いた接線の 長さは s である。他の2つの傍接円についても同様。 BL=BM, CL=CN より、 MANA = abc = 2s MA=NA より、 MA = NA = s 証明 図のように、面積を求める ABCの内接円および傍接円を描きます。ヘロンの公式で求めた面積は、他の方法で求めた面積と等しいはずだということを使います。 例 三角形の3辺の長さが,それぞれ13,14,15のとき,内接円の半径を求めなさい (答案) s=()/2=21 ヘロンの公式により、S= 他方,S=21r


ヘロンの公式の部屋
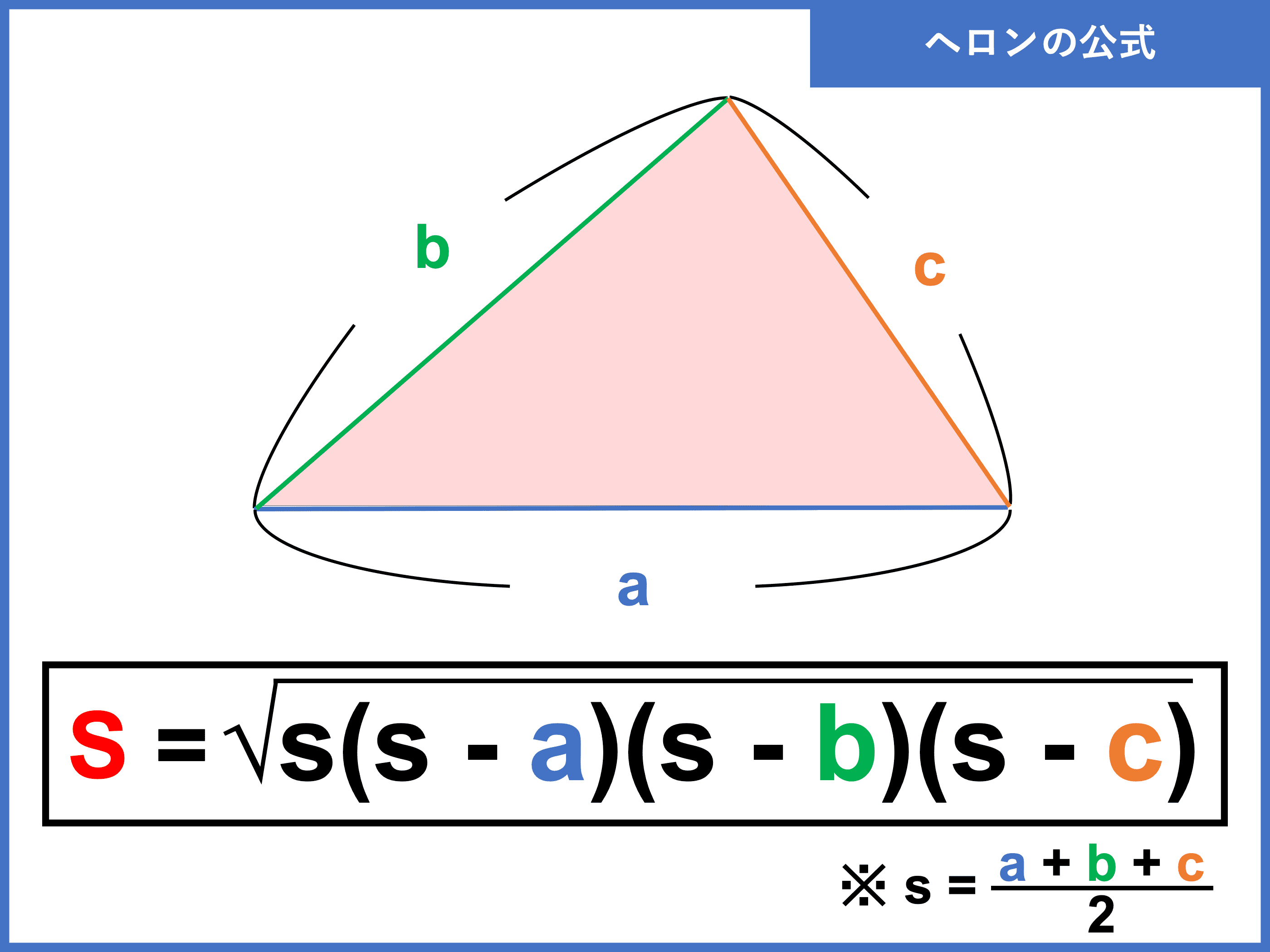
内接円の半径の公式を証明する方法は他にもあります。証明1に比べて計算も大変で筋が悪いですが, 全てを a, b, c a,b,c a, b, c で表す という方針でも証明できます。 証明 ・ヘロンの公式(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。Tooda Yuuto 18年10月13日 / 年3月6日 ヘロンの公式とは、三角形の3辺の長さ a, b, c を使って素早く三角形の面積を求める公式です。 3辺の長さが a, b, c の三角形の面積 S は S = s ( s − a) ( s − b) ( s − c) ただし、 ( た だ し 、 s = a b c 2) で求められる
この公式だと「3辺と内接円の半径から面積を計算する」ということをしています。 しかし、ヘロンの公式なら3辺から面積がわかります。 よって、3辺から内接円の半径を計算できることに気が付きます。さっそく計算してみると となります。概要 編集 この公式はアレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられるが、現代ではこれ自体はシラクサのアルキメデスにも既知であったと考えられていて、さらにそれ以前から知られていた可能性もある。 一般化として、円に内接する四角形ヘロンの公式 の用例・例文集 円の内接四角形の面積を求めるその式は、ヘロンの公式を内包している。ヘロンの公式はこれらの公式の特別な場合となっている。これは三角形におけるヘロンの公式を一般化したものである。これは三角形の面積を辺の長さで表すヘロンの公式と面積公式を
円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体円を使った証明の方法は三つあります(私が知っている限り)。 それらについて順番に紹介していきます。 三角形に内接する円を描いて証明する方法 まずは、三角形に内接する円を描いて証明する方法です。 以下の直角三角形を考えます。 この直角三角ABCの辺BCの外側に描いた傍接円において、頂点Aから引いた接線の 長さは s である。他の2つの傍接円についても同様。 BL=BM, CL=CN より、 MANA = abc = 2s MA=NA より、 MA = NA = s 証明 図のように、面積を求める ABCの内接円および傍接円を描きます。


三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ



ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri
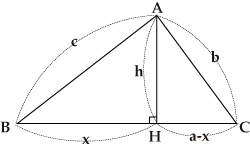
ヘロンの公式の証明には、 内接円の性質を利用した証明 と 三角関数を用いた証明 があります。 証明は少しむずかしいですが、証明方法を知ることでより理解が深まり、他の問題を解くときの手がかりにもなります。 さっそく、内接円の性質を利用した用して証明されるようなものまで幅広く定理や公式を載せてあります。利用の際の目安と なるよう定理や公式の重要度を以下のようなa,b,c,d の4 段階に分けてあります。 a 志望校を問わず全ての受験生が知っておくべきレベル(おそらく学校でも習う)(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。


三平方の定理とヘロン三角形の話


15年08月 怜悧玲瓏 高校数学を天空から俯瞰する
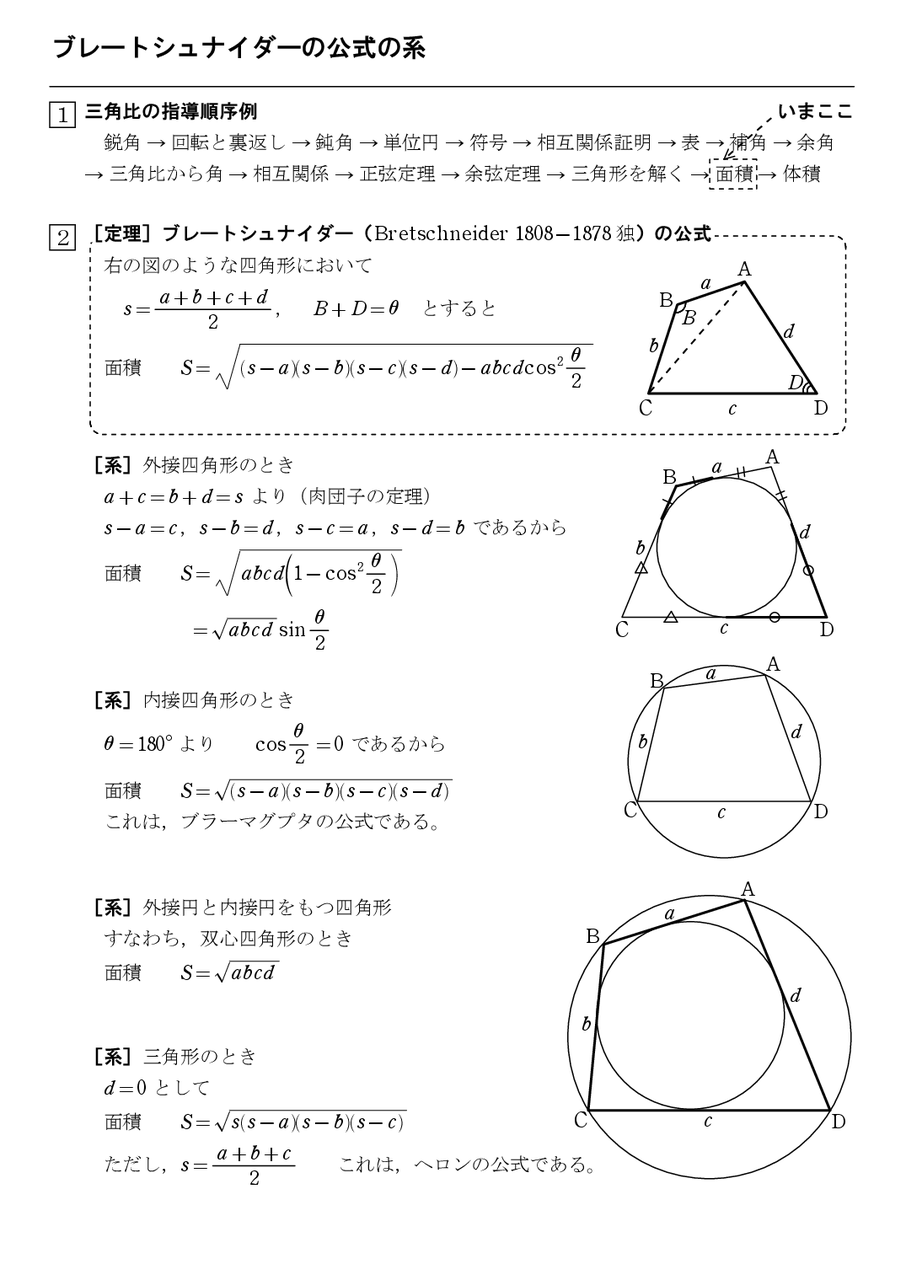
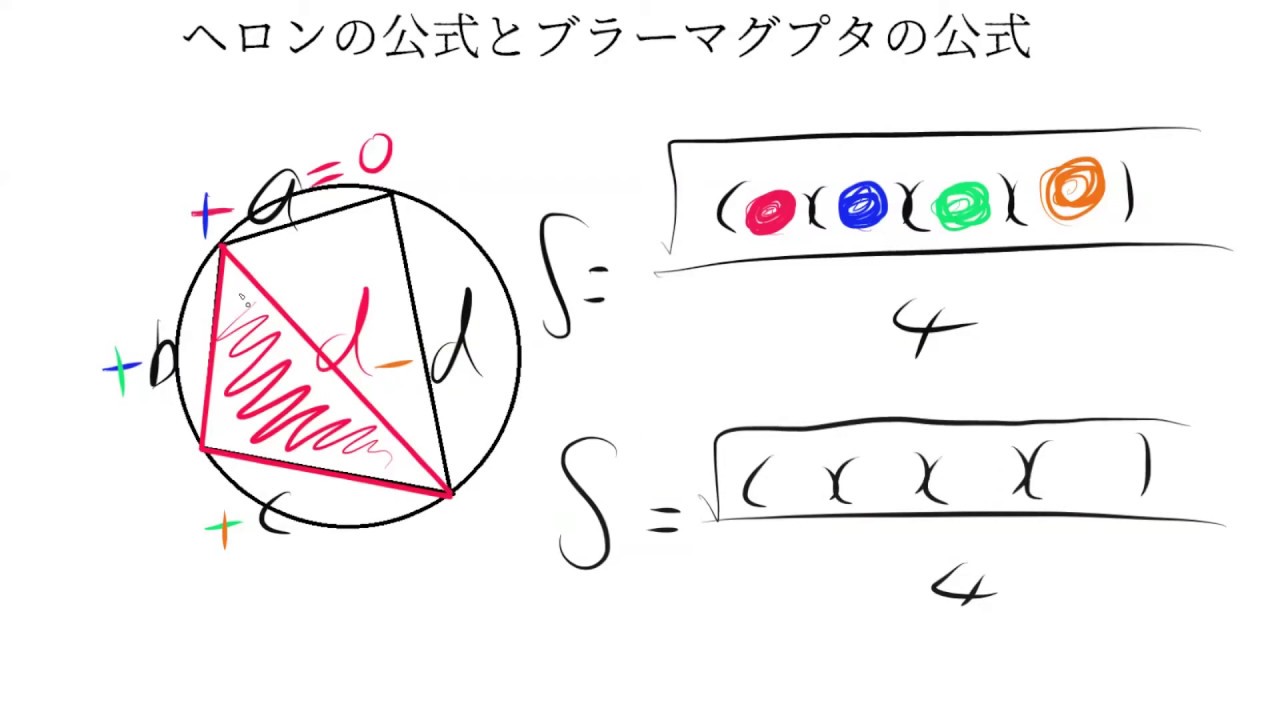
よって、ヘロンの公式でもブラーマグプタの公式でも、円に内接することは共通条件です。 また、ブラーマグプタの公式において一辺の長さ \(d\) を \(0\) とするとヘロンの公式と一致しますね。ヘロンの公式の証明(三角関数を使わずに) ヘロンの公式 は任意の 三角形 の3辺 a , b , c の長さから 面積S を求める 公式である 。 アレクサンドリアのヘロン が彼の著書『 Metrica 』の中で証明を与えていることから彼に帰せられる。よって、ヘロンの公式でもブラーマグプタの公式でも、円に内接することは共通条件です。 また、ブラーマグプタの公式において一辺の長さ \(d\) を \(0\) とするとヘロンの公式と一致しますね。


内接円の半径



100 ヘロン の 公式 中学 人気のある画像を投稿する
ヘロンの公式の証明と使用例 分野 平面図形 レベル ★ 基本公式 ヘロンの公式とは,三角形の3辺の長さから面積を求めるための公式です。 3辺の長さが a, b, c の三角形の面積 S は, s = a b c 2 と置くと, S = s ( s − a) ( s − b) ( s − c) で計算できる1 14 男 / 60歳以上 / エンジニア / 非常に役に立った /(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。


3分で分かる 三角形の内接円の半径の長さの求め方 公式 をわかりやすく 合格サプリ


コラム ヘロンの公式 江戸の数学
ヘロンの公式 三角形の面積を求める公式にヘロンの公式というものがあります。これまで 底辺×高さ÷2 サインを使って三角形の面積を求める公式 内接円をもつ三角形の面積を求める公式 と三角形の面積を求める公式をたくさん学んできましたが、数学内接円の練習問題 練習問題①「3 辺と面積から r を求める」内接円の半径の求め方例題 内接円の性質 性質①内心と各辺の距離 性質②角の二等分線と内心;



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ


コラム ヘロンの公式 江戸の数学
ブラマグプタの公式 円に内接する四角形の4辺の長さを、a、b、c、d とするとき、 ヘロンの公式、ブラマグプタの公式と、n角形(n=3、4)の面積を、その辺の長さのみを とる操作を通して、辺の長さで表現する一般の公式は存在しない。 証明は、次のAutoplay is paused You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to YouTube on your computer



三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ


A 13 B 14 C 15のとき Abcの内接円の半径rを求めたい Yahoo 知恵袋



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典



14年入試から数学ii 三角関数 2題 立命館大学 ヘロンの公式 札幌医科大学 内接円と外接円 の半径比 Uenotakato 上野尚人 イマイさん 数学講師 Note



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ


内接円



高校数学 円に内接する四角形の対角線の長さと面積 受験の月


Cosaは求まりましたが ヘロンの公式以外のやり方で面積を求めるやり方がわ Yahoo 知恵袋



ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri



円に内接する四角形の面積をサインを使って求める問題 数学i By ふぇるまー マナペディア



100 ヘロン の 公式 中学 人気のある画像を投稿する



3辺の長さが与えられたときの三角形の面積 中学 高校数学 身勝手な主張


内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典


3分で分かる 三角形の内接円の半径の長さの求め方 公式 をわかりやすく 合格サプリ



三角形の内接円の半径 ヘロンの公式 Youtube



ヘロンの公式 Instagram Posts Photos And Videos Picuki Com



高校数学 円に内接する四角形の面積ブラーマグプタの公式 裏技 の証明と円に内接しない四角形の面積ブレートシュナイダーの公式 裏技 受験の月



三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ



青い下線が引いてある問題の 半径rの求め方が分かりません 高校数学に関する質問 勉強質問サイト


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



悲報 教科書の公式は無駄すぎた 内接円 外接円の半径を最速で求める新公式 超わかる 高校数学 Youtube



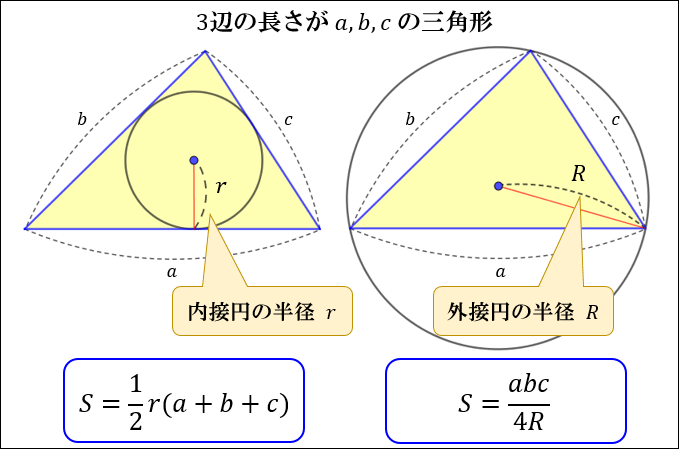
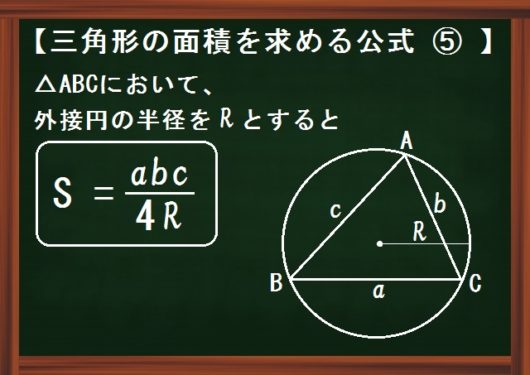
高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月


三角形の面積のヘロンの公式 ってやつですがこれって外接円に適用するもの Yahoo 知恵袋


ヘロンの公式の部屋



ブラーマグプタの公式 17年 大阪教育大 数学日和


ヘロンの公式の証明と使用例 高校数学の美しい物語



ヘロンの公式とは ヘロンノコウシキとは 単語記事 ニコニコ大百科



三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ


三平方の定理とヘロン三角形の話


ヘロンの公式の新着記事 アメーバブログ アメブロ


ヘロンの公式の部屋


ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式 Wikipedia
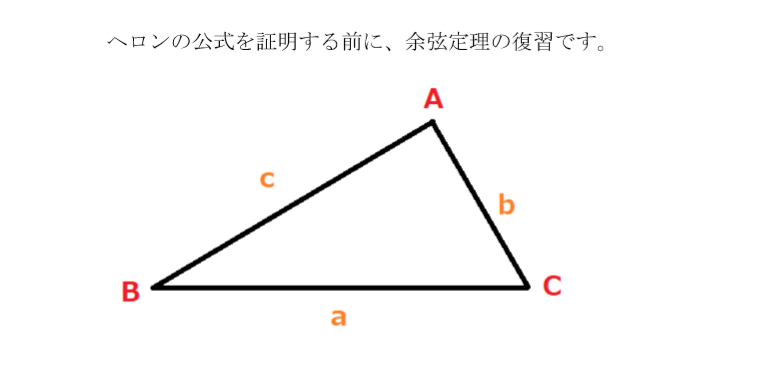


ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ


ヘロンの公式 思考力を鍛える数学


ヘロンの公式の簡単な証明はありますか Quora



100 ヘロン の 公式 中学 人気のある画像を投稿する



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ



重心の存在証明とヘロンの公式の証明 大阪教育大学10年後期数学第2問 理系のための備忘録


三角形の内接円 Geogebra
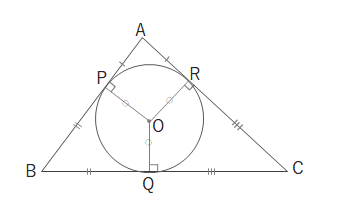


高校数学a 図形の性質 内接円と接線まとめと問題



ヘロンの公式 Instagram Posts Photos And Videos Picuki Com


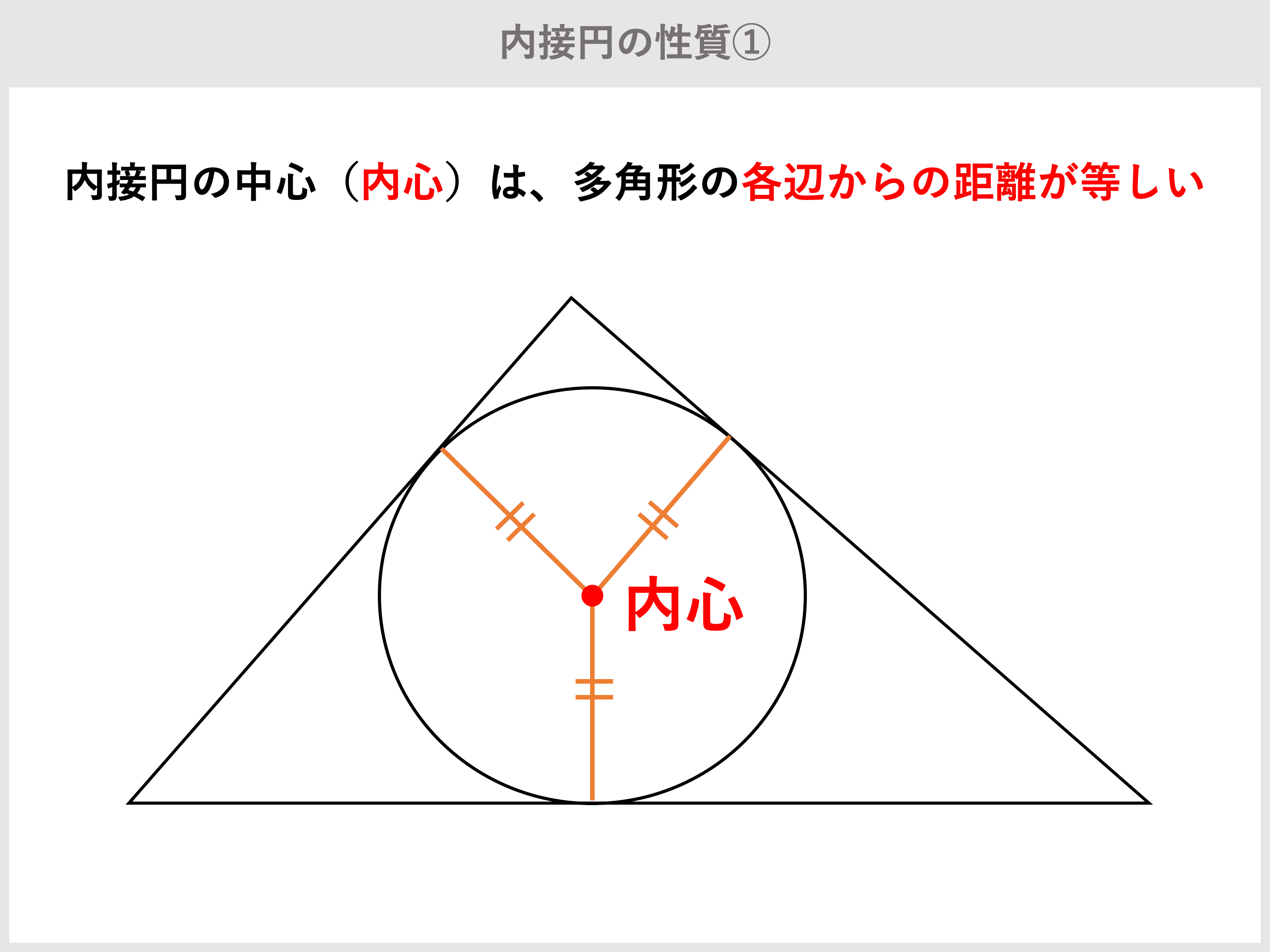
三角形とその内接円 および外接円の面積について考えてみる 内接円は 三角形のそれぞれの角の二等分線の交点から 各辺に垂線を降ろした線分を半径とした円です 内接円の半径 R は それぞれの角の二等分線より であり すべての R は



ヘロンの公式とは ヘロンの公式の証明と使い方 演習問題付き Himokuri



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
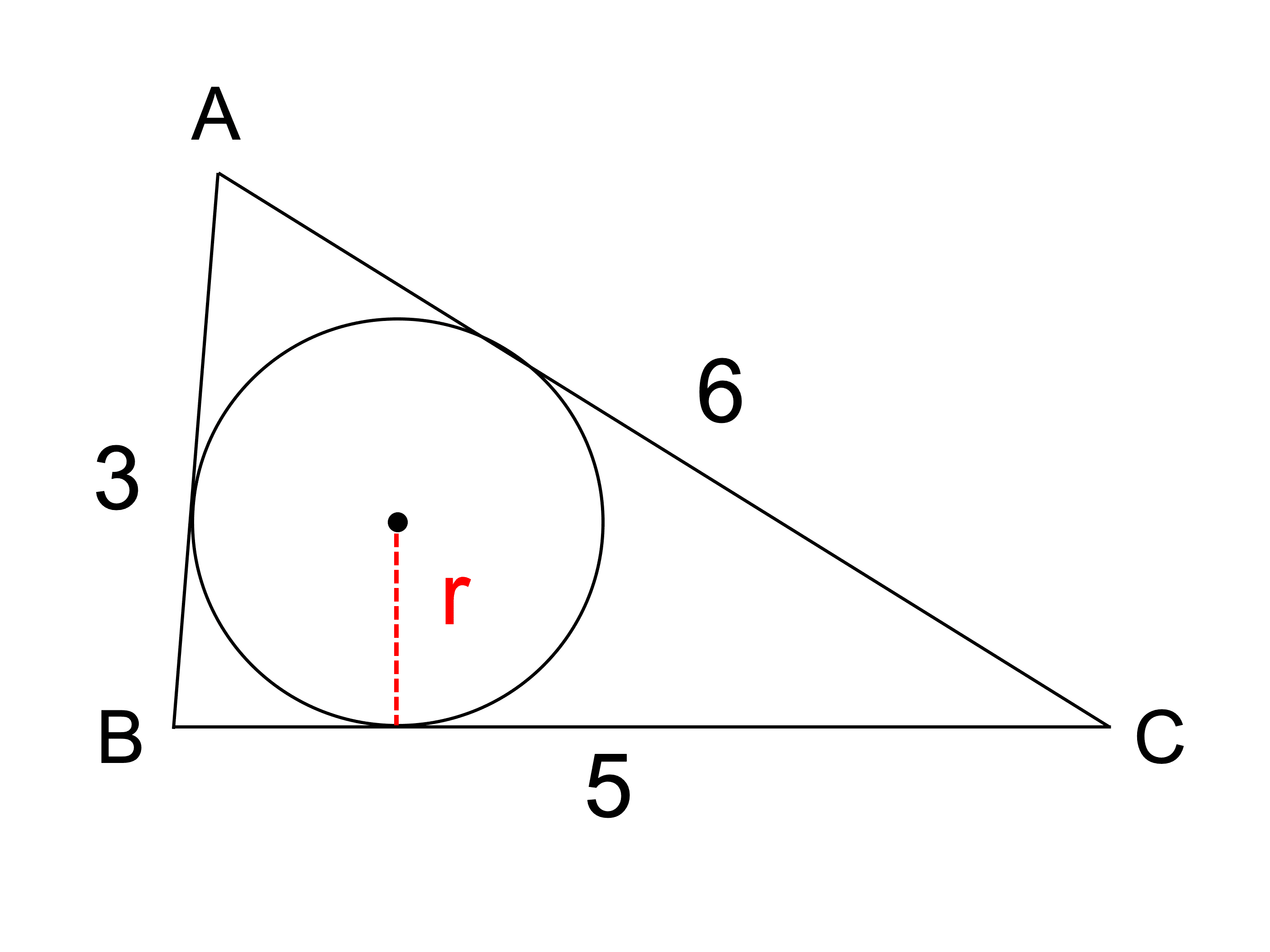


内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典


ヘロンの公式の簡単な証明はありますか Quora



中学 高校までの三角形の面積と面積比についてまとめました 高校生 数学のノート Clear


内接円の半径


ヘロンの公式の証明と使用例 高校数学の美しい物語


三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ


三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ


三角形の面積を求める公式7選 高校数学のまとめにどうぞ


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



三角形の中に接する半径の等しい2つの円 Okwave



ブラーマグプタの公式 17年 大阪教育大 数学日和


内接円の半径と三角形の面積 高校数学の美しい物語



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ



ヘロンの公式


ちょっと中学 高校数学 ヘロンの公式とブラーマグプタの公式 Youtube


ヘロンの公式の部屋



ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ


ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典



二等辺三角形の内接円 外接円に関する問題 2019年度前期日程の岡山大学文系の入試問題 身勝手な主張



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
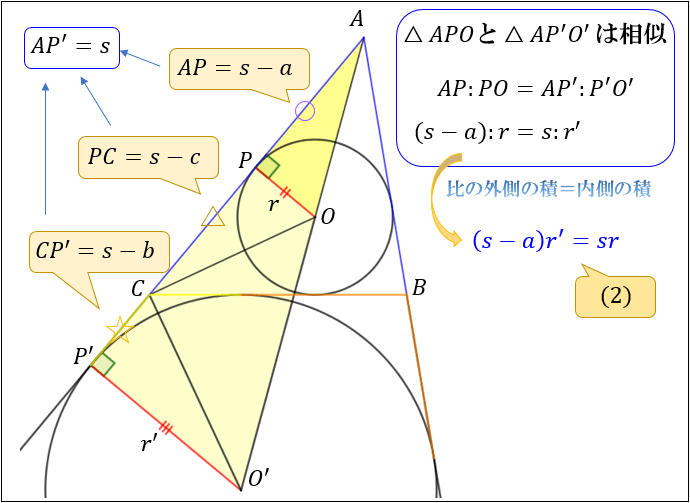


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ



内心 傍心と内接円 傍接円 ヤドカリの 気ままな数学



3分で分かる 三角形の内接円の半径の長さの求め方 公式 をわかりやすく 合格サプリ
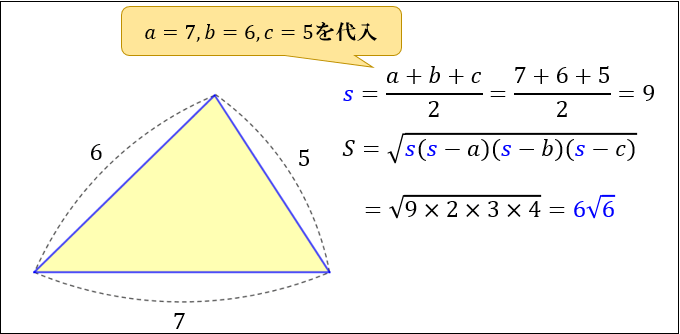


ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ


ヘロンの公式 三角形内接円の半径 Primeno S Diary



ヘロンの公式の新着記事 アメーバブログ アメブロ



三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ
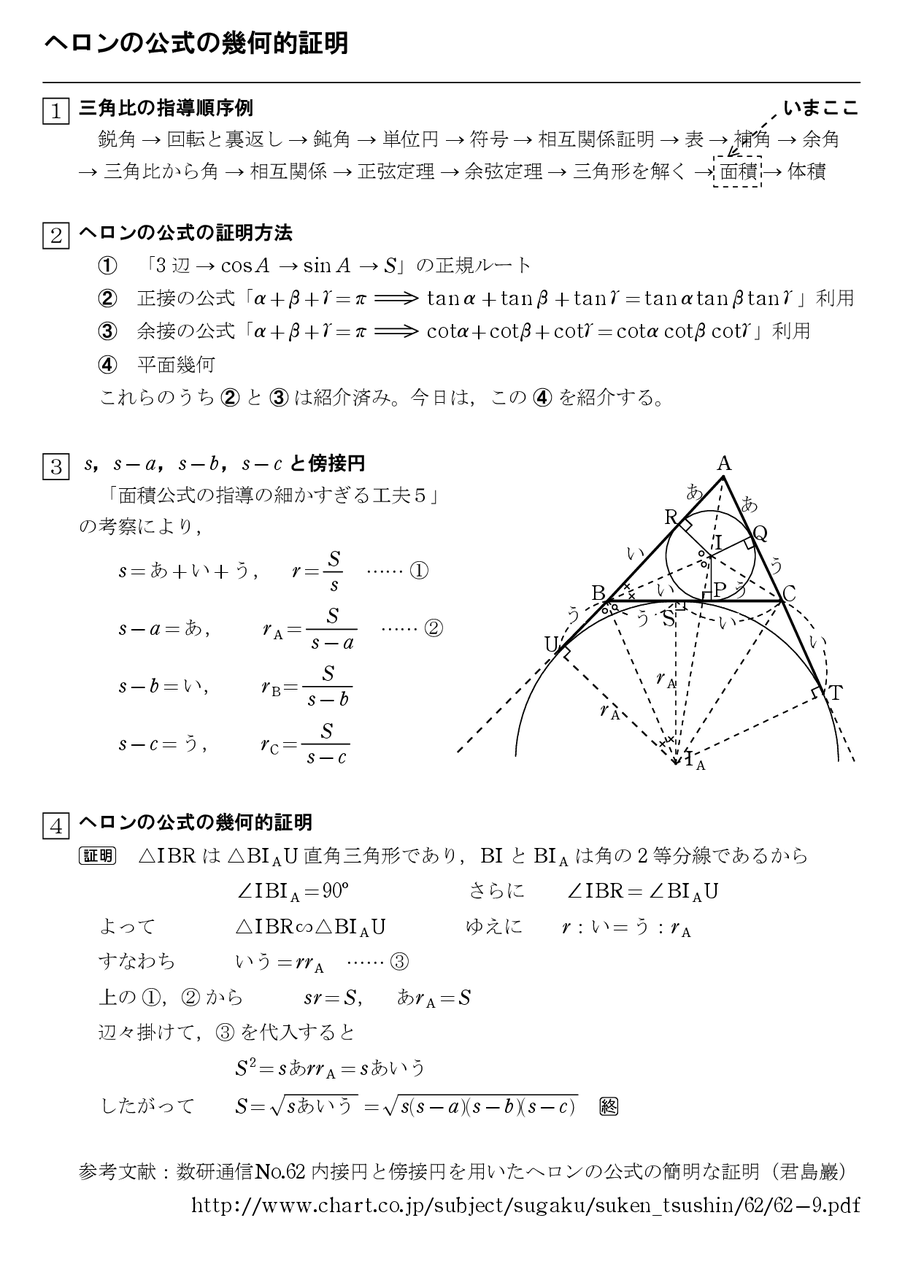


ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



三辺の長さが与えられた三角形の面積を求めるヘロンの公式の別証明 身勝手な主張



3辺の長さが与えられたときの三角形の面積 中学 高校数学 身勝手な主張



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



重心の存在証明とヘロンの公式の証明 大阪教育大学10年後期数学第2問 理系のための備忘録



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



高校数学の 三角形の外接円 内接円の半径 に関する問題を解いてみる Yahoo 知恵袋より Makelemonadejp Com



3分で分かる 三角形の内接円の半径の長さの求め方 公式 をわかりやすく 合格サプリ



3分で理解 ヘロンの公式の使い方をイチからていねいに解説 数スタ
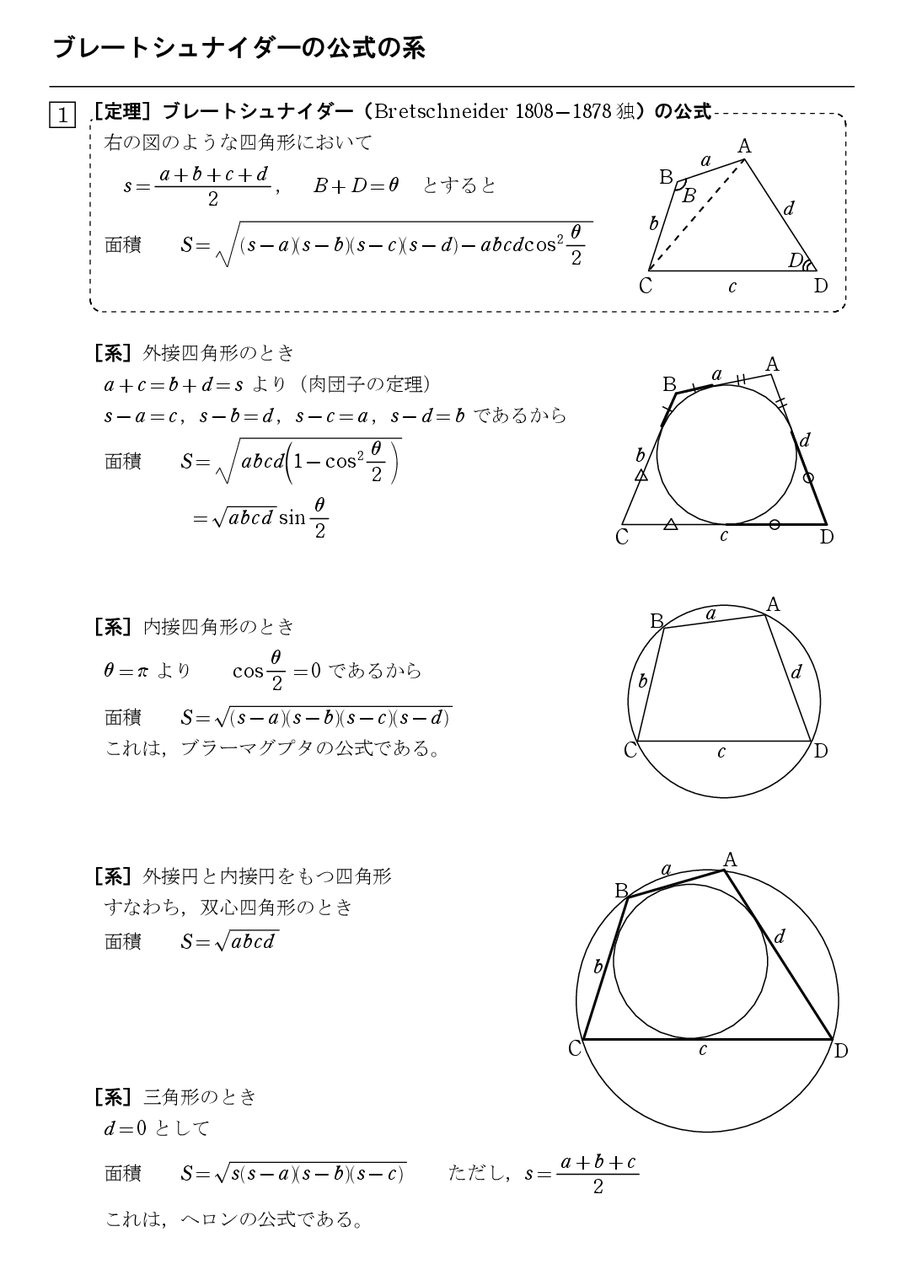


ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



No comments:
Post a Comment